Hello all,
Please cast your votes for the Hall of Famer of the month of February. Cast your votes under comments, please. Thank you. The first place will receive 5 bonus points, second place 4, third 3, fourth 2, and fifth 1.
Good Luck.
An interactive dialogue between students, parents, and mathematics teacher (Mr. Piatek) of the Maples Collegiate in Winnipeg, Manitoba, Canada. Please visit our blog frequently and post the information freely. "Imagination is more important than knowledge. Knowledge is limited. Imagination encircles the world." - Albert Einstein.
Monday, February 28, 2011
Thursday, February 24, 2011
Friday, February 18, 2011
General Solutions of Trigonometric Equations
Today in class we learned about General Solutions of Trigonometric Equations.
What we learned was that General Solutions of Trigonometric Equations are:
EXAMPLE of this type of equation

First step: Create your special triangle on unit circle

What we learned was that General Solutions of Trigonometric Equations are:
- Not bounded by an interval
- Have unlimited coterminal answers
- For each solution of sinθ or cosθ in degrees, add 360°k or 2kπ for radians
- For each solution of tanθ in degrees, add 180°k or kπ for radians
- Where kЄI (where k is an element of integers)
EXAMPLE of this type of equation

First step: Create your special triangle on unit circle
- Since tan is positive in quadrants 1 and 3, that's where we create our triangles

Second step: Figure out the angles for each quadrant they are in, making sure to add 360°or 180° or 2kπ or kπ
Q1 -> Ref. angle = Rel. angle
Q2 -> 180° - Ref. angle = Rel. angle
Q3 -> 180° + Ref. angle = Rel. angle
Q4 -> 360° - Ref. angle = Rel. angle
therefore
(in degrees)
Q1 = 30°+180°k, where kЄI
Q2 = 180°+30° = 210°+180°k, where kЄI
Q1 -> Ref. angle = Rel. angle
Q2 -> 180° - Ref. angle = Rel. angle
Q3 -> 180° + Ref. angle = Rel. angle
Q4 -> 360° - Ref. angle = Rel. angle
therefore
(in degrees)
Q1 = 30°+180°k, where kЄI
Q2 = 180°+30° = 210°+180°k, where kЄI
(in radians)
Q1 = π/6 + 2kπ
Q2 = 7π/6 + 2kπ
θ = π/6+2kπ , 7π/6+2kπ
where kЄI
Q1 = π/6 + 2kπ
Q2 = 7π/6 + 2kπ
θ = π/6+2kπ , 7π/6+2kπ
where kЄI
Thursday, February 17, 2011
Solving Trigonometric Equations on a Specified Interval 2
In this topic, it is the extension of what we've discussed the other day. We solved more examples to challenge our skills on it. Like solving for the Θ over the indicated interval.
Taking down notes from Mr. Piatek:
For example : 2sin 2 Θ - 3sinΘ - 1 over the interval 0 ≤ Θ ≤ 2π
Knowing how to factor:
2sin 2 Θ - 3sinΘ - 1 (we can say that sinΘ=x)
*** in this equation, we can say it as simple as 2x 2 - 3x + 1 = 0
To factor this : a = 2, b = -3, c = 1
then multiply: (a)(c) = (2)(1) = 2
*** Find two factors that of 2 that will add up to -3 (Find two numbers that when you multiply to 2 is positive and if you add will be negative)
Example: -2 and 1
= (-2)(1)
= 2
and -2 and -1
= (-2)(-1)
= -3
For the given example, 2sin 2 Θ - 3sinΘ - 1 over the interval 0 ≤ Θ ≤ 2π
Solution:
- (2sin 2 Θ)(sinΘ - 1)
- sinΘ = ½ sinΘ = 1
- sin 30° sin 90° = π/2
Find where sinΘ is positive,

Knowing now that it is in Q1 and Q2, draw a diagram having a reference angle of 30°,

As Q1 : Ref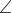 = Rel
= Rel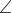
Θ = 30° / 30π/180° = π/6
As Q2 : π - Ref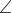
180° - 30° = 150° / 150π/180 = 10π/12 = 5π/6
Answer : Θ = π/6 , π/2 , 5π/6
NOTE: In using a calculator, be sure to set it to radians or degree if needed.
Wednesday, February 16, 2011
Hey Mr. P
I have a question with the worksheet; #6 & #18, I hope we could go over them in class. Thanks (:
Solving Trigonometric Equations on a Specified Interval
We started to study "Solving Trigonometric Equations on a Spcifid Interval" and it shows how to get θ in degrees or radians by using CAST rule.
FORMULA EVERY QUADRANT:
QI : Ref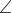 = Rel
= Rel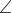
QII : 180 - Ref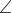 = Rel
= Rel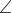
QIII: 180 + Ref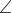 = Rel
= Rel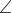
QIV: 360 - Ref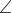 = Rel
= Rel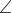
Example: 2cosθ + = 0 over the interval
= 0 over the interval 
Then diagram it and the reference angle should be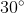 in QII and QIII because cosθ is (-) in QII and QII
in QII and QIII because cosθ is (-) in QII and QII
QII: 180 -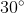 =
= 
QIII: 180 +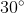 =
= 
 θ = {
θ = { ,
,  }
}
FORMULA EVERY QUADRANT:
QI : Ref
QII : 180 - Ref
QIII: 180 + Ref
QIV: 360 - Ref
Example: 2cosθ +
- 2cosθ +
= 0
- 2cosθ = -
: Transpose
and it should be -
: After transpose, divide both sides by 2 and,
: you will know now your cosθ
Then diagram it and the reference angle should be
QII: 180 -
QIII: 180 +
Tuesday, February 15, 2011
Special Angels and the Trigonometric fucntions 1
yesterday we have learn in class is about special angel and the trigonometric fucntions 1 to determine the exact value of trigonometric ratios for any multiples of 0°, 30°, 45°, 60° and 90° : as well as 0 , π/6 , π/4 , π/3 and π/2.
Six Trigonometric Functions
Sinθ = O/H Cscθ = H/O
Cosθ = A/H Secθ = H/A
Tanθ = O/A Cotθ = A/O
Special Angles - most angel on the unit circle are base on referenceangles of either 30°, 45° or 60°.
To find out solve the equation first. Select possible quadrant using CAST rule. Than check the interval given. By using the soh cah toa determine the reference angle by substituting the value of Sin θ = Opposite/Hypotenuse in a triangle in selected quadrant for this example. In last by using 3 simple steps we can find the related angle.
Six Trigonometric Functions
Sinθ = O/H Cscθ = H/O
Cosθ = A/H Secθ = H/A
Tanθ = O/A Cotθ = A/O
Special Angles - most angel on the unit circle are base on referenceangles of either 30°, 45° or 60°.
To find out solve the equation first. Select possible quadrant using CAST rule. Than check the interval given. By using the soh cah toa determine the reference angle by substituting the value of Sin θ = Opposite/Hypotenuse in a triangle in selected quadrant for this example. In last by using 3 simple steps we can find the related angle.
Saturday, February 12, 2011
The Unit Circle (part 2)
Last Friday we learned about the unit circle. Our formula in unit circle is X squared+ Y squared= 1. The standard position starts at (1,0).
In the CAST rule :
Quadrant I : sin(theta)- positive
cos(theta)-positive
tan(theta)-positive
Quadrant II : sin(theta)-positive
cos(theta)-negative
tan(theta)-negative
Quadrant III : sin(theta)-negative
cos(theta)-negative
tan(theta)-positive
Quadrant IV : sin(theta)-negative
cos(theta)-positive
tan(theta)-negative
Examples: 2 (stands for squared)
Find the sin(theta) in Quadrant I:
Given: (square root of 5, 2)
a2=b2=c2
square root of 5 squared=c2
5+4+c2
c2+square root of 9
=3
sin(theta)=O/H
=2/3
If (5/13, y) is a point on the unit circle in quadrant IV, find the value of y.
y=-12/13
The point P on the unit is NOT in Quadrant I. If sin(theta)=8/17, find the value of cos (theta).
cos (theta)=A/H
=-15/17
Find the tan(theta) in Quadrant II.
Given:(-4, 18)
tan(theta)=O/H
=-18/4 simplify: divide it to two.
=-9/2
Find the cos(theta) in Quadrant II.
given: (-3, 4)
cos(theta)= A/H
2 (stands for squared)
=a2+b2=c2
= -3 squared+ 4 squared=c2
=c2 square root= square root of 25
=5
cos(theta)= A/H
=-3/5
In the CAST rule :
Quadrant I : sin(theta)- positive
cos(theta)-positive
tan(theta)-positive
Quadrant II : sin(theta)-positive
cos(theta)-negative
tan(theta)-negative
Quadrant III : sin(theta)-negative
cos(theta)-negative
tan(theta)-positive
Quadrant IV : sin(theta)-negative
cos(theta)-positive
tan(theta)-negative
Examples: 2 (stands for squared)
Find the sin(theta) in Quadrant I:
Given: (square root of 5, 2)
a2=b2=c2
square root of 5 squared=c2
5+4+c2
c2+square root of 9
=3
sin(theta)=O/H
=2/3
If (5/13, y) is a point on the unit circle in quadrant IV, find the value of y.
y=-12/13
The point P on the unit is NOT in Quadrant I. If sin(theta)=8/17, find the value of cos (theta).
cos (theta)=A/H
=-15/17
Find the tan(theta) in Quadrant II.
Given:(-4, 18)
tan(theta)=O/H
=-18/4 simplify: divide it to two.
=-9/2
Find the cos(theta) in Quadrant II.
given: (-3, 4)
cos(theta)= A/H
2 (stands for squared)
=a2+b2=c2
= -3 squared+ 4 squared=c2
=c2 square root= square root of 25
=5
cos(theta)= A/H
=-3/5
Friday, February 11, 2011
Homework?
Hey Mr.P,
The assignment you said that was to be done over the weekend , is that found on the wiki?If not I'll just come and get it in the morning then finish it by class starts.
Thanks
The assignment you said that was to be done over the weekend , is that found on the wiki?If not I'll just come and get it in the morning then finish it by class starts.
Thanks
Thursday, February 10, 2011
The unit circle
The unit circle
In today's class we learned about unit circles. Unit circle is a circle with its centre at the origin and with a radius of one unit.
The equation for unit circle is: x squared+ y squared= one
A few class's ago we learned that positive distance is measured in a counter clock wise of a circle,and negative distance is measured in a clockwise of a circle.
we learned that the notation p(theta) is used to denote the terminal point,where the terminal arm of angle theta intercepts the unit circle, for every arc length theta on the unit circle, p(theta) is unique.
we can define p(theta) as the ordered pair p(x,y)
we were also reminded of SOH, CAH, TOA and what they stand for:
sin(theta)=opposite over hypotenuse
over hypotenuse
cos(theta)=adjacent over hypotenuse
tan(theta)=opposite over adjacent
using SOH ,CAH ,TOA we can found the p(theta) of an angle like we did in class,we found that:
sin(theta)=Y over 1 which sin(theta) equals Y
cos(theta)=X over 1 which cos(theta)equals X
tan(theta)=y over X
All that means is that the y axis is sin(theta) and x axis is cos(theta). Therefore, p(x,y)=p(cosO,sinO),and since the equation for unit circle is x squared+ y squared= one, it would be cos(squared) theta +sin(squared)theta=one.
And we were also reminded of the four quadrant and the rule of CAST.
quadrant 1 A quadrant 2 S quadrant 3 T quadrant 4 C
sin(theta) is + sin(theta) is + sin(theta) is _ sin(theta) is _
cos(theta) is + cos(theta) is _ cos(theta) is _ cos(theta) is +
tan(theta) is + tan(theta) is _ tan(theta) is + tan(theta) is _
Now one example of what we learned today is: where does p(theta) lie, given 0<2pi>
In today's class we learned about unit circles. Unit circle is a circle with its centre at the origin and with a radius of one unit.
The equation for unit circle is: x squared+ y squared= one
A few class's ago we learned that positive distance is measured in a counter clock wise of a circle,and negative distance is measured in a clockwise of a circle.
we learned that the notation p(theta) is used to denote the terminal point,where the terminal arm of angle theta intercepts the unit circle, for every arc length theta on the unit circle, p(theta) is unique.
we can define p(theta) as the ordered pair p(x,y)
we were also reminded of SOH, CAH, TOA and what they stand for:
sin(theta)=opposite
 over hypotenuse
over hypotenuse
cos(theta)=adjacent over hypotenuse
tan(theta)=opposite over adjacent
using SOH ,CAH ,TOA we can found the p(theta) of an angle like we did in class,we found that:
sin(theta)=Y over 1 which sin(theta) equals Y
cos(theta)=X over 1 which cos(theta)equals X
tan(theta)=y over X
All that means is that the y axis is sin(theta) and x axis is cos(theta). Therefore, p(x,y)=p(cosO,sinO),and since the equation for unit circle is x squared+ y squared= one, it would be cos(squared) theta +sin(squared)theta=one.
And we were also reminded of the four quadrant and the rule of CAST.
quadrant 1 A quadrant 2 S quadrant 3 T quadrant 4 C
sin(theta) is + sin(theta) is + sin(theta) is _ sin(theta) is _
cos(theta) is + cos(theta) is _ cos(theta) is _ cos(theta) is +
tan(theta) is + tan(theta) is _ tan(theta) is + tan(theta) is _
Now one example of what we learned today is: where does p(theta) lie, given 0
Tuesday, February 8, 2011
Feb. 8th Monday
Today we learned how to convert degrees into radian and radian into degrees.
To convert degrees into radian you must multiply by pi/180.
To convert radian into degrees you must multiply by 180/pi.
Somtime when converting degrees into radian you will get #pi/#. If this happens you must reduce the two #'s as far as possilbe.
Sorry I didnt put any example...I'm feeble and i dont know how to on this :( and i couldnt find the pi sign so i just had to spell it lol
To convert degrees into radian you must multiply by pi/180.
To convert radian into degrees you must multiply by 180/pi.
Somtime when converting degrees into radian you will get #pi/#. If this happens you must reduce the two #'s as far as possilbe.
Sorry I didnt put any example...I'm feeble and i dont know how to on this :( and i couldnt find the pi sign so i just had to spell it lol
Monday, February 7, 2011
360 Degrees
There is 360 degrees in a circle because the sumerians invented it for writing back in 3000 BC. But back in 2400 they made a calender that divided 12 months into 30 days each. The sumerians saw the sun,moon and other planets moving around in that degree. That is where the origin of 360 came from!
why are there 360 degrees in a circle?
 |
| Add caption |
Subscribe to:
Posts (Atom)