Solving Trigonometric Equations on a Specified Interval 2

In this topic, it is the extension of what we've discussed the other day. We solved more examples to challenge our skills on it. Like solving for the Θ over the indicated interval.

Taking down notes from Mr. Piatek:

For example : 2sin ² Θ - 3sinΘ - 1 over the interval 0 ≤ Θ ≤ 2π

Knowing how to factor:

2sin ² Θ - 3sinΘ - 1 (we can say that sinΘ=x)

*** in this equation, we can say it as simple as 2x ² - 3x + 1 = 0

To factor this : a = 2, b = -3, c = 1

then multiply: (a)(c) = (2)(1) = 2

*** Find two factors that of 2 that will add up to -3 (Find two numbers that when you multiply to 2 is positive and if you add will be negative)

Example: -2 and 1

= (-2)(1)

= 2

and -2 and -1

= (-2)(-1)

= -3

For the given example, 2sin ² Θ - 3sinΘ - 1 over the interval 0 ≤ Θ ≤ 2π

Solution:

- (2sin ² Θ)(sinΘ - 1)

- sinΘ = ½ sinΘ = 1

- sin 30° sin 90° = π/2

Find where sinΘ is positive,

Knowing now that it is in Q1 and Q2, draw a diagram having a reference angle of 30°,

As Q1 : Ref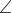 = Rel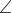

Θ = 30° / 30π/180° = π/6

As Q2 : π - Ref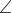

180° - 30° = 150° / 150π/180 = 10π/12 = 5π/6

Answer : Θ = π/6 , π/2 , 5π/6

NOTE: In using a calculator, be sure to set it to radians or degree if needed.